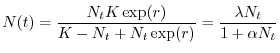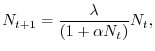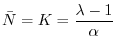Subsections
Uno dei modelli più utilizzati per descrivere la dinamica di popolazioni
a riproduzione concentrata con dipendenza da densità è stato
introdotto da Beverton e Holt (1957) con riferimento agli stock ittici.
L'idea sulla quale si sono basati è schematizzata in Fig. 2.
Figura 2:
Schema sintetico dei processi alla base del modello di Beverton-Holt
|
![\includegraphics[width=0.75\linewidth]{beverton}](img393.gif) |
Si indichino con 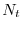 il numero di adulti (o di femmine adulte se la
popolazione è sessuata) che costituiscono la popolazione della stagione
il numero di adulti (o di femmine adulte se la
popolazione è sessuata) che costituiscono la popolazione della stagione
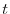 -esima. Si supponga che ciascun adulto abbia fertilità
-esima. Si supponga che ciascun adulto abbia fertilità 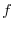 , così che
il numero di uova (o di uova da cui nasceranno femmine) complessivamente
presenti nella popolazione è pari a
, così che
il numero di uova (o di uova da cui nasceranno femmine) complessivamente
presenti nella popolazione è pari a
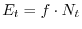 . Dopo la deposizione
delle uova tutti gli adulti riproduttori muoiono come nel caso della
cavalletta. Non tutte le uova deposte dagli
. Dopo la deposizione
delle uova tutti gli adulti riproduttori muoiono come nel caso della
cavalletta. Non tutte le uova deposte dagli 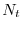 individui si schiudono
con successo e non tutti gli avannotti da esse originati
sopravvivono fino allo stadio di giovani pesci dando origine a giovani individui.
L'ipotesi introdotta da Beverton e Holt è che la sopravvivenza da uovo a giovane
pesce
individui si schiudono
con successo e non tutti gli avannotti da esse originati
sopravvivono fino allo stadio di giovani pesci dando origine a giovani individui.
L'ipotesi introdotta da Beverton e Holt è che la sopravvivenza da uovo a giovane
pesce
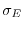 sia, a causa della competizione per utilizzo di risorse comuni, decrescente in
maniera non lineare con la densità delle uova medesime, come illustrato
in Fig. 3. Il parametro
sia, a causa della competizione per utilizzo di risorse comuni, decrescente in
maniera non lineare con la densità delle uova medesime, come illustrato
in Fig. 3. Il parametro
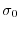 rappresenta la
sopravvivenza dallo stadio di uovo a quello di giovane in condizioni di
scarso affollamento, mentre il parametro
rappresenta la
sopravvivenza dallo stadio di uovo a quello di giovane in condizioni di
scarso affollamento, mentre il parametro 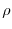 regola l'entità della
dipendenza da densità. In seguito, solo una frazione
regola l'entità della
dipendenza da densità. In seguito, solo una frazione
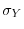 degli
degli 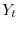 giovani presenti riuscirà ad emergere come
adulto alla stagione successiva.
giovani presenti riuscirà ad emergere come
adulto alla stagione successiva.
Figura 3:
La sopravvivenza delle uova nel modello di Beverton-Holt
è supposta decrescere con la densità delle uova stesse.
|
![\includegraphics[scale=0.75]{sigma_bev}](img400.gif) |
Se ne conclude dunque che il legame tra il numero di adulti presenti in due
stagioni consecutive è il seguente
ovvero, rinominando per semplicità i parametri, cioè ponendo
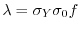 e
e
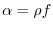 , si
ottiene il seguente modello di Beverton-Holt
, si
ottiene il seguente modello di Beverton-Holt
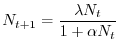 |
(8.1) |
Il parametro 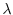 rappresenta il massimo tasso di crescita della
popolazione in condizioni di non affollamento, cioè in assenza di
competizione, mentre
rappresenta il massimo tasso di crescita della
popolazione in condizioni di non affollamento, cioè in assenza di
competizione, mentre 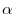 misura la forza della competizione
intraspecifica. Dalla soluzione del modello logistico presentato in
precedenza, si può facilmente riconoscere che, se si considera come
istante iniziale l'anno
misura la forza della competizione
intraspecifica. Dalla soluzione del modello logistico presentato in
precedenza, si può facilmente riconoscere che, se si considera come
istante iniziale l'anno 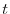 -esimo e come istante finale l'anno (
-esimo e come istante finale l'anno (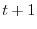 )-esimo, la
soluzione del modello logistico diviene
)-esimo, la
soluzione del modello logistico diviene
a patto di porre
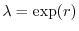 e
e
![$ \alpha=[\exp(r)-1]/K$](img406.gif) . Possiamo quindi
dire che il modello di Beverton-Holt è l'analogo in tempo discreto del
modello logistico.
. Possiamo quindi
dire che il modello di Beverton-Holt è l'analogo in tempo discreto del
modello logistico.
Prima di procedere con l'analisi dei comportamenti di un modello discreto
come quello appena ricavato, è bene fare alcune riflessioni di carattere
generale sulla natura dei modelli a tempo discreto per popolazioni regolate.
In analogia con quanto visto per il modello malthusiano per popolazioni a
riproduzione concentrata, che ha la forma
possiamo scrivere il modello di Beverton-Holt come
che è della forma
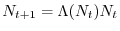 |
(8.2) |
Il termine
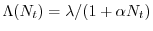 rappresenta
pertanto il tasso finito di crescita della popolazione, che però non
è più costante, come nel caso di dinamica malthusiana, ma è una
funzione decrescente della densità. La ricerca di soluzioni stazionarie (o equilibri) nel caso
di modelli discreti della forma (12) si traduce non più nella ricerca di
soluzioni per cui la derivata
rappresenta
pertanto il tasso finito di crescita della popolazione, che però non
è più costante, come nel caso di dinamica malthusiana, ma è una
funzione decrescente della densità. La ricerca di soluzioni stazionarie (o equilibri) nel caso
di modelli discreti della forma (12) si traduce non più nella ricerca di
soluzioni per cui la derivata 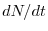 si annulla, bensì nella ricerca delle
soluzioni per cui sia
si annulla, bensì nella ricerca delle
soluzioni per cui sia
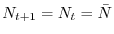 . L'equilibrio cosiddetto banale
del modello (12) è
. L'equilibrio cosiddetto banale
del modello (12) è 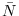 = 0. Si noti che la
condizione
= 0. Si noti che la
condizione
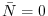 corrisponde all'estinzione e risulta dunque importante
comprendere sotto quali condizioni tale equilibrio (cosiddetto banale) è
stabile. Gli equilibri non banali del modello (12) sono le soluzioni
dell'equazione
corrisponde all'estinzione e risulta dunque importante
comprendere sotto quali condizioni tale equilibrio (cosiddetto banale) è
stabile. Gli equilibri non banali del modello (12) sono le soluzioni
dell'equazione
Nel caso del modello di Beverton-Holt (11), dalla condizione
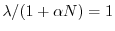 si ricava
si ricava
valore che, come vedremo fra poco, corrisponde alla capacità portante
della popolazione. Questo valore ha senso biologico solo se
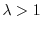 ,
altrimenti assumerebbe valori negativi. Dobbiamo quindi supporre che
la popolazione abbia a basse densità un tasso finito di crescita
maggiore di 1. D'altra parte l'estinzione
,
altrimenti assumerebbe valori negativi. Dobbiamo quindi supporre che
la popolazione abbia a basse densità un tasso finito di crescita
maggiore di 1. D'altra parte l'estinzione 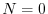 è uno stato di equilibrio
instabile se
è uno stato di equilibrio
instabile se
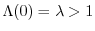 . Se
. Se
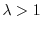 ,
infatti, è sufficiente che la densità sia di poco superiore a zero,
che la popolazione comincerà a crescere. Si può invece dimostrare che
,
infatti, è sufficiente che la densità sia di poco superiore a zero,
che la popolazione comincerà a crescere. Si può invece dimostrare che
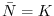 è uno stato di equilibrio stabile. Si noti che
è uno stato di equilibrio stabile. Si noti che
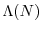 è una funzione
decrescente: il tasso finito di crescita, nell'ipotesi appena avanzata che a
basse densità esso sia maggiore di 1, diventa unitario proprio per
è una funzione
decrescente: il tasso finito di crescita, nell'ipotesi appena avanzata che a
basse densità esso sia maggiore di 1, diventa unitario proprio per 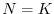 .
Pertanto, se nel generico anno
.
Pertanto, se nel generico anno 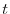 -esimo
-esimo 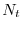 è inferiore alla
capacità portante, allora
è inferiore alla
capacità portante, allora
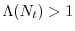 , e la popolazione del
seguente anno (
, e la popolazione del
seguente anno (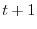 )-esimo sarà più abbondante. Se al contrario
)-esimo sarà più abbondante. Se al contrario
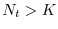 , allora
, allora
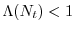 e la popolazione dell'anno (
e la popolazione dell'anno (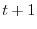 )-esimo
sarà più scarsa. È possibile dimostrare che, nel caso del
modello di Beverton-Holt, qualunque sia il valore non nullo
dell'abbondanza iniziale della popolazione, nel lungo periodo la popolazione
si assesterà alla capacità portante
)-esimo
sarà più scarsa. È possibile dimostrare che, nel caso del
modello di Beverton-Holt, qualunque sia il valore non nullo
dell'abbondanza iniziale della popolazione, nel lungo periodo la popolazione
si assesterà alla capacità portante 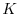 . Possiamo comprendere questo
fatto con una semplice costruzione grafica: il diagramma di Moran.
. Possiamo comprendere questo
fatto con una semplice costruzione grafica: il diagramma di Moran.
![]() il numero di adulti (o di femmine adulte se la
popolazione è sessuata) che costituiscono la popolazione della stagione
il numero di adulti (o di femmine adulte se la
popolazione è sessuata) che costituiscono la popolazione della stagione
![]() -esima. Si supponga che ciascun adulto abbia fertilità
-esima. Si supponga che ciascun adulto abbia fertilità ![]() , così che
il numero di uova (o di uova da cui nasceranno femmine) complessivamente
presenti nella popolazione è pari a
, così che
il numero di uova (o di uova da cui nasceranno femmine) complessivamente
presenti nella popolazione è pari a
![]() . Dopo la deposizione
delle uova tutti gli adulti riproduttori muoiono come nel caso della
cavalletta. Non tutte le uova deposte dagli
. Dopo la deposizione
delle uova tutti gli adulti riproduttori muoiono come nel caso della
cavalletta. Non tutte le uova deposte dagli ![]() individui si schiudono
con successo e non tutti gli avannotti da esse originati
sopravvivono fino allo stadio di giovani pesci dando origine a giovani individui.
L'ipotesi introdotta da Beverton e Holt è che la sopravvivenza da uovo a giovane
pesce
individui si schiudono
con successo e non tutti gli avannotti da esse originati
sopravvivono fino allo stadio di giovani pesci dando origine a giovani individui.
L'ipotesi introdotta da Beverton e Holt è che la sopravvivenza da uovo a giovane
pesce
![]() sia, a causa della competizione per utilizzo di risorse comuni, decrescente in
maniera non lineare con la densità delle uova medesime, come illustrato
in Fig. 3. Il parametro
sia, a causa della competizione per utilizzo di risorse comuni, decrescente in
maniera non lineare con la densità delle uova medesime, come illustrato
in Fig. 3. Il parametro
![]() rappresenta la
sopravvivenza dallo stadio di uovo a quello di giovane in condizioni di
scarso affollamento, mentre il parametro
rappresenta la
sopravvivenza dallo stadio di uovo a quello di giovane in condizioni di
scarso affollamento, mentre il parametro ![]() regola l'entità della
dipendenza da densità. In seguito, solo una frazione
regola l'entità della
dipendenza da densità. In seguito, solo una frazione
![]() degli
degli ![]() giovani presenti riuscirà ad emergere come
adulto alla stagione successiva.
giovani presenti riuscirà ad emergere come
adulto alla stagione successiva.
![\includegraphics[scale=0.75]{sigma_bev}](img400.gif)
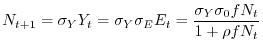
![]() rappresenta il massimo tasso di crescita della
popolazione in condizioni di non affollamento, cioè in assenza di
competizione, mentre
rappresenta il massimo tasso di crescita della
popolazione in condizioni di non affollamento, cioè in assenza di
competizione, mentre ![]() misura la forza della competizione
intraspecifica. Dalla soluzione del modello logistico presentato in
precedenza, si può facilmente riconoscere che, se si considera come
istante iniziale l'anno
misura la forza della competizione
intraspecifica. Dalla soluzione del modello logistico presentato in
precedenza, si può facilmente riconoscere che, se si considera come
istante iniziale l'anno ![]() -esimo e come istante finale l'anno (
-esimo e come istante finale l'anno (![]() )-esimo, la
soluzione del modello logistico diviene
)-esimo, la
soluzione del modello logistico diviene