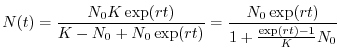Subsections
Si consideri una popolazione animale con riproduzione continua la cui
dinamica, in condizioni di non affollamento, possa essere ben descritta da
un modello malthusiano continuo (si veda il paragrafo 6.4) con tasso
intrinseco di crescita positivo, pari ad 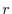 . Si assuma inoltre che:
. Si assuma inoltre che:
- gli animali si muovono in maniera casuale in un habitat di dimensione fissa;
- la probabilità che due animali si incontrino è proporzionale al
quadrato della densità di animali presenti e quindi a
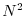 . Tale
assunzione è del tutto simile a quella che si adotterebbe in una
cinetica chimica del secondo ordine, in cui la probabilità di reazione
è proporzionale al quadrato della concentrazione del reagente;
. Tale
assunzione è del tutto simile a quella che si adotterebbe in una
cinetica chimica del secondo ordine, in cui la probabilità di reazione
è proporzionale al quadrato della concentrazione del reagente;
- la probabilità che tre o più individui si incontrino
contemporaneamente è trascurabile;
- ogni volta che due individui si incontrano, tale incontro produce una
diminuzione della natalità e/o un aumento della mortalità. In altre
parole, un aumento nella densità di individui presenti si traduce in una
diminuzione del tasso di crescita della popolazione
Traducendo in equazioni le ipotesi appena avanzate, si ottiene l'equazione
seguente
dove 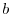 è un coefficiente costante e positivo,
detto coefficiente di competizione intraspecifica, che tiene conto in
maniera aggregata sia della mobilità di ciascun individuo che del danno
prodotto da ciascun incontro.
è un coefficiente costante e positivo,
detto coefficiente di competizione intraspecifica, che tiene conto in
maniera aggregata sia della mobilità di ciascun individuo che del danno
prodotto da ciascun incontro.
A basse densità, cioè se 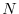 è piccolo, il termine
è piccolo, il termine 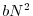 è
trascurabile rispetto ad
è
trascurabile rispetto ad 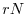 . Una popolazione costituita da uno sparuto numero
di individui tende dunque inizialmente a crescere in maniera esponenziale.
Al crescere di
. Una popolazione costituita da uno sparuto numero
di individui tende dunque inizialmente a crescere in maniera esponenziale.
Al crescere di 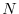 , tuttavia, il termine
, tuttavia, il termine 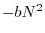 diventa sempre più
rilevante e, essendo negativo, provoca una diminuzione del tasso di crescita
della popolazione. È facile comprendere che, se
diventa sempre più
rilevante e, essendo negativo, provoca una diminuzione del tasso di crescita
della popolazione. È facile comprendere che, se 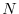 è sufficientemente
elevato, tale termine di competizione può prevalere sul termine di
accrescimento malthusiano (
è sufficientemente
elevato, tale termine di competizione può prevalere sul termine di
accrescimento malthusiano (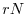 ), causando un'inversione nel segno della
derivata rispetto al tempo
), causando un'inversione nel segno della
derivata rispetto al tempo 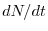 . In particolare, il valore di
. In particolare, il valore di 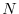 per cui si
annulla
per cui si
annulla 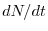 è
è
Il parametro 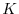 , chiamato capacità portante, è molto importante da un punto di vista
ecologico, poiché, come mostreremo nel successivo paragrafo, rappresenta
la densità di equilibrio globalmente stabile per la popolazione. In
altre parole, qualunque sia la densità iniziale non nulla della
popolazione, nel lungo periodo essa si assesta a
, chiamato capacità portante, è molto importante da un punto di vista
ecologico, poiché, come mostreremo nel successivo paragrafo, rappresenta
la densità di equilibrio globalmente stabile per la popolazione. In
altre parole, qualunque sia la densità iniziale non nulla della
popolazione, nel lungo periodo essa si assesta a 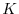 . Questo spiega anche il
termine ``capacità portante'': si intende infatti la ``capacità portante
dell'ambiente'' cioè il massimo numero di individui che un determinato
ambiente ospitante la popolazione può contenere nel lungo periodo. Si
noti che
. Questo spiega anche il
termine ``capacità portante'': si intende infatti la ``capacità portante
dell'ambiente'' cioè il massimo numero di individui che un determinato
ambiente ospitante la popolazione può contenere nel lungo periodo. Si
noti che 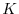 è inversamente proporzionale a
è inversamente proporzionale a 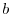 , cioè è tanto minore
quanto maggiore è la competizione fra gli individui. Nel caso limite di
assenza di competizione, il modello logistico si riduce a quello
malthusiano.
, cioè è tanto minore
quanto maggiore è la competizione fra gli individui. Nel caso limite di
assenza di competizione, il modello logistico si riduce a quello
malthusiano.
Prima di procedere all'analisi della soluzione del modello logistico,
occorre rilevare che la forma matematica più popolare di tale modello,
introdotta dallo statistico belga Verhulst nel 1838 e riscoperta negli anni
venti del XX secolo dai demografi Pearl e Read, è la seguente
In analogia con quanto visto per il modello malthusiano, si può
individuare nel termine 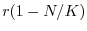 il tasso netto istantaneo di crescita pro
capite,
il tasso netto istantaneo di crescita pro
capite,
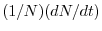 , ovvero il contributo medio che ogni individuo dà alla
crescita della popolazione. A differenza del caso malthusiano, tale
parametro non è qui costante, ma dipende dalla densità della
popolazione. Esso è massimo per
, ovvero il contributo medio che ogni individuo dà alla
crescita della popolazione. A differenza del caso malthusiano, tale
parametro non è qui costante, ma dipende dalla densità della
popolazione. Esso è massimo per 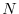 tendente a zero e decresce linearmente
con la densità, fino ad annullarsi per
tendente a zero e decresce linearmente
con la densità, fino ad annullarsi per 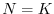 .
.
La soluzione del modello logistico ha andamento sigmoide, come mostrato
dalla linea a tratto continuo nella Fig. 1
Figura 1:
Dati relativi all'accrescimento della pecora (Ovis aries)
in Tasmania. A tratto continuo è rappresentata una soluzione del modello
logistico.
|
![\includegraphics[width=0.75\linewidth]{pecora}](img388.gif) |
I punti riportati nello stesso grafico rappresentano i dati relativi alla
pecora della Tasmania (si veda ancora la Fig. 1). Dopo l'introduzione della specie
all'inizio del 1800 in quest'isola a sud dell'Australia, la popolazione si
è accresciuta dapprima in maniera esponenziale rallentando poi la
crescita sino a raggiungere un regime stazionario. L'andamento
dell'abbondanza è ben approssimato dal modello logistico.
Per ottenere la soluzione del modello logistico attraverso simulazione si
può utilizzare un qualunque software commerciale che integra equazioni
differenziali con metodi numerici. Nel caso specifico del modello logistico,
tuttavia, è possibile ottenere una soluzione analitica dell'equazione e
ricavare così l'espressione che permette di calcolare in maniera
esplicita il valore di 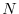 al tempo
al tempo  a partire dalla densità iniziale
a partire dalla densità iniziale
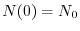 :
:
È facile verificare che per qualsiasi condizione iniziale 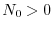 si ha
che
si ha
che 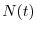 tende alla capacità portante
tende alla capacità portante 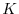 per
per
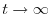 .
.
![]() . Si assuma inoltre che:
. Si assuma inoltre che:
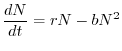
![]() è piccolo, il termine
è piccolo, il termine ![]() è
trascurabile rispetto ad
è
trascurabile rispetto ad ![]() . Una popolazione costituita da uno sparuto numero
di individui tende dunque inizialmente a crescere in maniera esponenziale.
Al crescere di
. Una popolazione costituita da uno sparuto numero
di individui tende dunque inizialmente a crescere in maniera esponenziale.
Al crescere di ![]() , tuttavia, il termine
, tuttavia, il termine ![]() diventa sempre più
rilevante e, essendo negativo, provoca una diminuzione del tasso di crescita
della popolazione. È facile comprendere che, se
diventa sempre più
rilevante e, essendo negativo, provoca una diminuzione del tasso di crescita
della popolazione. È facile comprendere che, se ![]() è sufficientemente
elevato, tale termine di competizione può prevalere sul termine di
accrescimento malthusiano (
è sufficientemente
elevato, tale termine di competizione può prevalere sul termine di
accrescimento malthusiano (![]() ), causando un'inversione nel segno della
derivata rispetto al tempo
), causando un'inversione nel segno della
derivata rispetto al tempo ![]() . In particolare, il valore di
. In particolare, il valore di ![]() per cui si
annulla
per cui si
annulla ![]() è
è
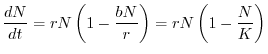
![\includegraphics[width=0.75\linewidth]{pecora}](img388.gif)
![]() al tempo
al tempo ![]() a partire dalla densità iniziale
a partire dalla densità iniziale
![]() :
: