Proprietà del modello di Leslie

Il modello di Leslie gode di due proprietà di particolare importanza che riportiamo qui senza dimostrazione. La prima proprietà è che nel lungo periodo, ovvero esauritasi l'influenza della condizione iniziale $\mathbf{n}_{0}$, la popolazione, anche se strutturata in classi, tende ad una crescita esponenziale come le popolazioni non strutturate di cui al Capitolo 6. Tale crescita è caratterizzata da un tasso finito di crescita $\lambda$, sia per quanto riguarda la crescita di ciascuna classe d'età, ovvero

$$n_{x}(t+1) = \lambda n_{x}(t)$$

sia per quanto riguarda la crescita della popolazione nel suo complesso:

$$N(t+1) = \lambda N(t)$$

dove $N(t)=\sum_{x} n_{x}(t)$ è il numero totale di femmine nella popolazione. Ovviamente la popolazione si estingue, è stazionaria, o esplode a seconda che sia $\lambda<1$, $\lambda=1$, $\lambda>1$.

Il valore di $\lambda$ può essere calcolato in vari modi. Molto semplicemente si può ricavare $\lambda$ tramite simulazione dell'equazione (10): è infatti sufficiente ricavare l'abbondanza della popolazione nel tempo ($N(1)$, $N(2)$, $N(3)$, ...) e valutare i rapporti $N(t+1)/N(t)$. Simulando la dinamica della popolazione il cui grafo di vita è riprodotto in Fig. 4 e a partire dalla condizione iniziale $n_{0}$ scelta in precedenza, i rapporti $N(t+1)/N(t)$ si assestano ad un valore costante, approssimativamente pari a 1.33, come mostrato in Fig. 5. Prima di raggiungere una dinamica esponenziale, la popolazione può fluttuare in modo più o meno irregolare per qualche anno. Solo dopo un certo periodo di tempo, tanto più lungo quanto più grande è $m$ (il numero di classi d'età) e quanto più $\lambda$ è prossimo a 1, la popolazione segue un andamento esponenziale con tasso finito di crescita pari a $\lambda$.

Figura 5: Andamento nel tempo del rapporto tra l'abbondanza della popolazione in un anno $t+1$-esimo e nel precedente anno $t$-esimo per le popolazioni di Fig. 4.

La seconda proprietà di cui gode il modello di Leslie è che nel lungo periodo la proporzione di individui in ciascuna classe d'età tende a diventare costante nel tempo, indipendentemente dalle condizioni iniziali. In altri termini, se definiamo distribuzione per età l'insieme delle $m$ grandezze

$$\pi_{x}(t)=\frac{n_{x}(t)}{N(t)}$$

cioè la frazione di individui nella popolazione che hanno età $x$ al tempo $t$, si ha che $\pi_{x}(t)$ diventa, per $t$ molto grande, funzione della sola età degli individui e non anche del tempo ( $\pi_{x}(t)\quad\to \pi_{x}$). Ne consegue, pertanto, che il numero di individui nella classe d'età $x$ al tempo $t$ può essere calcolato come il prodotto di due fattori

$$n_{x}(t)=N(t)\pi_{x}$$

Il primo fattore, $N(t)$, è funzione solo del tempo e varia secondo la legge $N(t+1) = \lambda N(t)$ mentre il secondo fattore, $\pi_{x}$, è funzione della sola età $x$. Si dice allora che la popolazione ha raggiunto la distribuzione stabile d'età. Tale distribuzione viene definita stabile proprio perché la popolazione, sul lungo periodo, tende ad essere strutturata secondo tale distribuzione indipendentemente dalle condizioni iniziali.

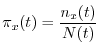
La distribuzione stabile d'età può essere calcolata semplicemente tramite simulazione, come mostrato in Fig.6.

Figura 6: Dinamica della distribuzione per età di una popolazione strutturata in tre classi come in Fig. 5.