Da un punto di vista matematico, è facile tradurre le informazioni
riportate nel grafo di vita in un modello. Le variabili del
modello sono indicate con ![]() e rappresentano il numero di femmine che
nell'anno
e rappresentano il numero di femmine che
nell'anno ![]() hanno età
hanno età ![]() . Esse sono tante quante sono i nodi del grafo di
vita: nell'esempio presentato prima avremo pertanto tre variabili:
. Esse sono tante quante sono i nodi del grafo di
vita: nell'esempio presentato prima avremo pertanto tre variabili:
![]() ,
, ![]() e
e ![]() .
.
Invecchiamento: se si indica con ![]() la sopravvivenza annuale
di una femmina di età
la sopravvivenza annuale
di una femmina di età ![]() , l'equazione che descrive la dinamica delle
femmine che hanno più di un anno di età (
, l'equazione che descrive la dinamica delle
femmine che hanno più di un anno di età (![]() ) è la seguente
) è la seguente
Tradotta in parole essa suona così: ``le femmine che nell'anno ![]() hanno
età
hanno
età ![]() sono le sopravvissute fra tutte quelle che nell'anno
sono le sopravvissute fra tutte quelle che nell'anno ![]() avevano
età
avevano
età ![]() ''. Con riferimento al nostro esempio, essendo
''. Con riferimento al nostro esempio, essendo
![]() e
e
![]() , possiamo dunque scrivere
, possiamo dunque scrivere
Riproduzione: l'equazione che descrive la dinamica delle femmine di
un anno di età è invece più complessa. Se è vero, infatti,
che ``le femmine che hanno età 1 nell'anno ![]() sono le sopravvissute fra
quelle che avevano età 0 nell'anno
sono le sopravvissute fra
quelle che avevano età 0 nell'anno ![]() '' occorre specificare quante sono le
nuove nate nell'anno
'' occorre specificare quante sono le
nuove nate nell'anno ![]() . Con riferimento al problema proposto, dal momento
che:
. Con riferimento al problema proposto, dal momento
che:
Nella sua forma completa, il modello che descrive compiutamente la dinamica della nostra popolazione è esprimibile attraverso le tre equazioni
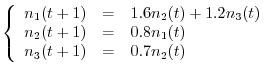
![$\displaystyle M = \left[
\begin{array}{ccc}
0 & 1.6 & 1.2\\
0.8 & 0 & 0 \\
0 & 0.7 & 0
\end{array}
\right]
$](img346.gif)
In generale, la matrice di Leslie ha tante righe e colonne quante sono le
classi d'età (quindi 3 nel nostro esempio). Per una popolazione generica
con ![]() classi d'età la matrice di Leslie è del tipo:
classi d'età la matrice di Leslie è del tipo:
![$\displaystyle M = \left[
\begin{array}{ccccc}
s_0 f_1& s_0 f_2 & \cdots & s_0...
... & \ddots & 0 & 0 \\
0 & 0 & \cdots & {s_{m-1}} & 0 \\
\end{array} \right]
$](img348.gif)
Se, nel caso del nostro esempio, la popolazione nell'anno 0 fosse costituita da 40 femmine di un anno di età, nessuna di due anni e 20 di tre anni di età, ovvero
![$\displaystyle \mathbf{n}_0 = \left[
\begin{array}{l}
40\\
0\\
20
\end{array} \right]
$](img353.gif)
![$\displaystyle \mathbf{n}_1 = M \cdot \mathbf{n}_0 =
\left[\begin{array}{ccc}
...
...rray}\right]
=
\left[\begin{array}{l}
24\\
32\\
0
\end{array}\right]
$](img354.gif)
![$\displaystyle n_2 = \left[\begin{array}{ccc}
0 & 1.6 & 1.2\\
0.8 & 0 & 0 \\ ...
...ght]
= \left[\begin{array}{l}
51.2 \\
19.2 \\
22.4
\end{array}\right]
$](img355.gif)