Seguendo l'approccio proposto da Leslie alla fine degli anni '40, Lefkovitch
propose verso la metà degli anni '60 un modello più generale, che si
mostra particolarmente utile in tutti quei casi in cui i parametri
demografici della popolazione dipendono non tanto dall'età quanto dallo
stadio di sviluppo degli individui. Ci sono diverse ragioni per le quali
può essere conveniente adottare questa prospettiva, ad esempio in tutti
quei casi in cui:
- la sopravvivenza e la fertilità degli individui, piuttosto che
dall'età, dipendono dalla taglia o, più in generale, sono
determinabili in base a criteri che consentono di classificare la
popolazione in stadi diversi;
- è difficile (se non addirittura impossibile) stimare con precisione
l'età degli individui della specie considerata;
- gli individui possono eventualmente rivisitare alcuni degli stadi di
sviluppo già attraversati (ad esempio, parti di una pianta possono
essere divorate da organismi erbivori o morire a causa di condizioni
ambientali avverse riportando le piante a un precedente stadio).
Con riferimento alla nozione di grafo di vita definita in precedenza è
semplice capire la struttura di un modello a stadi di sviluppo. I passi
fondamentali sono i seguenti:
- Scegliere un intervallo temporale di evoluzione da uno stadio ad un altro;
- Identificare gli stadi del ciclo vitale e definire un nodo per ciascuno di
essi;
- Connettere tramite un arco un nodo con un altro nodo se e solo se
esiste la possibilità di transire direttamente dall'uno all'altro
in un singolo passo temporale;
- Etichettare ogni arco del grafo con un coefficiente che rappresenti la
probabilità di transizione o il successo riproduttivo (nel caso di archi
che conducano allo stadio di vita iniziale).
Così come si è fatto nel caso del modello di Leslie, è facile
descrivere il grafo di vita mediante una matrice
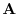 che consenta di
calcolare l'abbondanza, in un determinato anno, degli individui appartenenti
a ciascuno degli stadi di sviluppo in funzione delle abbondanze nell'anno
precedente
che consenta di
calcolare l'abbondanza, in un determinato anno, degli individui appartenenti
a ciascuno degli stadi di sviluppo in funzione delle abbondanze nell'anno
precedente
dove
![$ \mathbf{n(t)}= [n_{1}(t) \quad n_{2}(t) \ldots n_{m}(t)]^{T}$](img374.gif) è un vettore colonna il cui elemento
è un vettore colonna il cui elemento 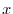 -esimo rappresenta l'abbondanza di
individui allo stadio di sviluppo
-esimo rappresenta l'abbondanza di
individui allo stadio di sviluppo 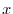 -esimo al tempo
-esimo al tempo  . Da un punto di vista
modellistico, la trattazione non cambia in modo significativo: la differenza
principale rispetto al modello di Leslie è che la matrice
. Da un punto di vista
modellistico, la trattazione non cambia in modo significativo: la differenza
principale rispetto al modello di Leslie è che la matrice
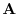 di
transizione demografica può avere qualsiasi elemento diverso da zero (e
non più solo la prima riga per le fertilità e la sottodiagonale
principale per le sopravvivenze, come accadeva per
di
transizione demografica può avere qualsiasi elemento diverso da zero (e
non più solo la prima riga per le fertilità e la sottodiagonale
principale per le sopravvivenze, come accadeva per
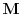 ), in quanto,
almeno in teoria, può sempre esserci una probabilità non nulla di
transizione da uno stadio di sviluppo a qualsiasi altro stadio. La
proprietà di accrescimento malthusiano caratterizza anche i modelli a
struttura di taglia, così come l'esistenza di una struttura stabile di
taglia. A titolo di esempio, considerate i problemi 1.22,
1.23 e 1.24 dell'eserciziario.
), in quanto,
almeno in teoria, può sempre esserci una probabilità non nulla di
transizione da uno stadio di sviluppo a qualsiasi altro stadio. La
proprietà di accrescimento malthusiano caratterizza anche i modelli a
struttura di taglia, così come l'esistenza di una struttura stabile di
taglia. A titolo di esempio, considerate i problemi 1.22,
1.23 e 1.24 dell'eserciziario.