Subsections
Il primo passo per capire come varia nel tempo la densità di una
popolazione è quello di scrivere un'equazione di bilancio su 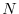 fra la stagione
fra la stagione  e la
stagione
e la
stagione 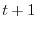 . Questo bilancio può essere
formulato nel modo seguente: il numero di individui al tempo
. Questo bilancio può essere
formulato nel modo seguente: il numero di individui al tempo 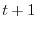 è pari a quello al tempo
è pari a quello al tempo  cui bisogna
cui bisogna
- sottrarre gli individui morti (
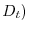 ;
;
- aggiungere gli individui nati durante la stagione
 e sopravvissuti fino
alla stagione
e sopravvissuti fino
alla stagione 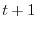 (
(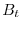 );
);
- sottrarre gli individui emigrati durante la stagione
 (
(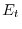 );
);
- aggiungere gli individui immigrati nello stesso periodo (
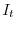 ).
).
Figura 1:
Schema dei fattori principali che influenzano lo
stato di una popolazione.
|
![\includegraphics[scale=0.6]{schema}](img212.gif) |
Possiamo quindi scrivere
Sebbene nascite e immigrazioni contribuiscano ad aumentare il numero di
individui della popolazione da una stagione a quella successiva, mentre
morti ed emigrazioni lo fanno diminuire, la natura di questi processi
è profondamente diversa. Il numero di nascite e morti dipende infatti
solo dall'abbondanza della popolazione nello specifico ambiente in cui essa
si trova. Le immigrazioni, al contrario, dipendono in genere da elementi
esterni alla popolazione, come la presenza di un ``serbatoio'' di individui
nelle aree limitrofe alla popolazione in esame. Le emigrazioni possono
essere influenzate invece sia da elementi intrinseci, in quanto in
condizioni di eccessivo affollamento gli individui possono essere
incentivati a emigrare, sia da elementi estrinseci, come la presenza di siti
adatti verso cui emigrare facilmente. Per semplicità, nel seguito si
assumerà che immigrazione ed emigrazione siano trascurabili rispetto a
natalità e mortalità: la popolazione cui faremo riferimento deve
dunque pensarsi come distribuita omogeneamente nello spazio e in condizioni
di isolamento rispetto ad eventuali popolazioni limitrofe. Lo studio degli
effetti di fenomeni di dispersione va infatti al di là degli scopi del
presente corso.
[l]![\includegraphics[scale=0.25]{malthus}](img214.gif) Attraverso un esempio concreto (la dinamica della cavalletta) e un problema
proposto (la dinamica della cinciallegra) capiremo come utilizzare
l'equazione di bilancio per formulare il più semplice modello di
popolazione: quello malthusiano, così chiamato in onore di T. R. Malthus, il
fondatore della moderna demografia. Esso prevede un andamento esponenziale
dell'abbondanza di una popolazione e si basa sull'ipotesi fondamentale che
le capacità di sopravvivere e di riprodursi di ciascun individuo non
siano influenzate dalla presenza di altri individui della stessa specie.
Attraverso un esempio concreto (la dinamica della cavalletta) e un problema
proposto (la dinamica della cinciallegra) capiremo come utilizzare
l'equazione di bilancio per formulare il più semplice modello di
popolazione: quello malthusiano, così chiamato in onore di T. R. Malthus, il
fondatore della moderna demografia. Esso prevede un andamento esponenziale
dell'abbondanza di una popolazione e si basa sull'ipotesi fondamentale che
le capacità di sopravvivere e di riprodursi di ciascun individuo non
siano influenzate dalla presenza di altri individui della stessa specie.
Un esempio concreto ci aiuterà a capire come si costruisce un modello di
dinamica di popolazioni a partire dall'equazione di bilancio. Prendiamo in
esame il caso specifico della cavalletta dei prati, Chorthippus brunneus
(Fig. 2).
Figura 2:
Un esemplare di cavalletta dei prati.
|
![\includegraphics[scale=.4]{cavalletta}](img215.gif) |
I parametri demografici essenziali che descrivono gli elementi salienti del
ciclo di vita della cavalletta possono essere schematicamente riassunti in
questo modo:
- tutti gli adulti muoiono nell'arco di un anno;
- ogni femmina depone mediamente 7.3 ooteche alla fine dell'estate;
- ogni teca contiene circa 11 uova;
- le uova rimangono in uno stato di quiescenza durante l'inverno e solo il
7.9% di esse si schiude all'inizio della primavera successiva per dar
luogo a ninfe nello stadio di sviluppo I;
- il 72% delle ninfe nello stadio I passa allo stadio II;
- il 76% dallo stadio II a quello III, e ancora il 76% dallo stadio III
al IV;
- l'89% delle ninfe allo stadio IV emerge finalmente come cavalletta adulta
pronta a riprodursi
- il rapporto sessi si può in prima approssimazione assumere pari a 1:1
(cioè il 50% degli individui sono femmine e il 50% maschi);
Per la popolazione di cavallette la lunghezza di una generazione è
quindi pari ad un anno. Dal momento che gli adulti si riproducono una sola
volta e poi muoiono all'inizio dell'inverno, si parla di specie univoltina e
annuale. Ogni generazione sopravvive per un solo anno e nello stesso istante di
tempo non ci sono individui che appartengono a generazioni diverse. Si dice
quindi che le generazioni non si sovrappongono.
Siccome nessun adulto nell'anno  sopravvive fino all'anno
successivo, il numero di individui nella generazione
sopravvive fino all'anno
successivo, il numero di individui nella generazione 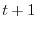 sarà dato solo
dagli individui nati nella generazione
sarà dato solo
dagli individui nati nella generazione  che sopravvivono fino alla
generazione
che sopravvivono fino alla
generazione 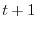 . Avendo indicato con
. Avendo indicato con 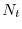 il numero di cavallette (maschi +
femmine) all'inizio della generazione
il numero di cavallette (maschi +
femmine) all'inizio della generazione  , conviene costruire il modello per
passi successivi:
, conviene costruire il modello per
passi successivi:
numero di femmine della generazione  : : |
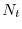 /2 /2 |
| numero di teche prodotte: |
7.3  num. femmine = 3.65 num. femmine = 3.65 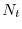 |
| numero di uova: |
11  num. teche = 11 num. teche = 11 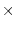 3.65 3.65 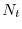 = 40.15 = 40.15 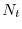 |
| num. ninfe stadio I: |
0.079 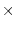 40.15 40.15 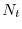 = 3.172 = 3.172 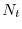 |
| num. ninfe stadio II: |
0.72 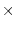 3.172 3.172 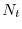 = 2.284 = 2.284 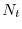 |
| Num. ninfe stadio III: |
0.76  2.284 2.284 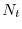 = 1.736 = 1.736  |
| num. ninfe stadio IV: |
0.76 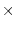 1.736 1.736 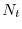 = 1.319 = 1.319 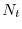 |
Num. adulti generaz. 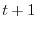 : : |
0.89 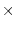 1.319 1.319 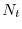 = 1.174 = 1.174 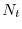 |
In breve, la dinamica della popolazione di cavallette è compiutamente
descritta dalla semplice equazione:
Il fattore 1.174 prende il nome di tasso finito di crescita, di seguito indicato con 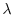 .
Ad ogni generazione, quindi, la popolazione di cavallette aumenta di oltre il
17%: se quest'anno la popolazione ha 100 individui, l'anno prossimo ne avrà
circa 117, fra due 137, e così via (come mostrato nella Fig. 3).
.
Ad ogni generazione, quindi, la popolazione di cavallette aumenta di oltre il
17%: se quest'anno la popolazione ha 100 individui, l'anno prossimo ne avrà
circa 117, fra due 137, e così via (come mostrato nella Fig. 3).
Figura 3:
Andamento nel tempo del numero di cavallette
a partire dal numero iniziale di 100 individui
|
![\includegraphics[width=0.7\linewidth]{serie_cavallette}](img217.gif) |
Un incremento medio annuo superiore al 15% è già di per sé
tutt'altro che trascurabile, ma può sembrare relativamente piccolo se
confrontato con la grande fertilità delle cavallette (ogni femmina
produce in media più di 80 uova!). In realtà solo una piccola
frazione di uova emerge come adulto alla generazione successiva: infatti
neanche l'8% riesce a schiudersi e a raggiungere il primo stadio di
ninfa, e poco più di un terzo delle ninfe di tipo I (0.72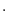 0.76
0.76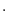 0.76
0.76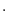 0.89=0.37) raggiunge lo stadio di adulto
riproduttivo.
0.89=0.37) raggiunge lo stadio di adulto
riproduttivo.
Proviamo ora ad affrontare un problema leggermente più complesso, quello
della dinamica di popolazione della cinciallegra Parus major (un esemplare è mostrato
nella Fig. 4).
Il ciclo di vita della cinciallegra può essere schematizzato in questo modo:
- le femmine adulte depongono in media 10 uova all'inizio dell'estate
- l'84% delle uova si schiude e dà luogo a pulcini che sopravvivono
fino al primo mese di vita
- il 71% dei pulcini si impiuma e raggiunge i tre mesi di vita
- solo il 10% dei pulcini impiumati sopravvive all'inverno ed emerge come
adulto riproduttivo l'anno successivo
- il rapporto sessi è circa 1:1 (50% maschi e 50% femmine)
- il 50% degli adulti muore durante l'inverno, la parte rimanente
sopravvive fino all'estate dell'anno successivo.
Questo caso differisce da quello delle precedente delle cavallette
perché non tutti gli adulti muoiono durante l'inverno ma una frazione
consistente di essi riesce a sopravvivere da un anno all'altro e a
riprodursi nuovamente. La popolazione all'inizio dell'estate è composta
pertanto da cinciallegre che sono nate in anni diversi e che appartengono,
quindi, a diverse generazioni. Le nascite sono sempre sincronizzate, e
avvengono in una stagione riproduttiva precisa e ben definita durante
l'anno, ma gli adulti possono vivere relativamente a lungo e quindi le
generazioni, per quanto discrete, ora si sovrappongono. Sareste in grado, avendo come traccia
la linea di cui all'esempio precedente, di descrivere attraverso un modello
la dinamica di questa specie? Verificate la vostra soluzione con quella
proposta alla pagina esercizi/cincia.htm raggiungibile dalla homepage
del corso.
Figura 4:
Una cinciallegra (Parus major)
|
![\includegraphics[scale=.7]{cincia}](img218.gif) |
![]() fra la stagione
fra la stagione ![]() e la
stagione
e la
stagione ![]() . Questo bilancio può essere
formulato nel modo seguente: il numero di individui al tempo
. Questo bilancio può essere
formulato nel modo seguente: il numero di individui al tempo ![]() è pari a quello al tempo
è pari a quello al tempo ![]() cui bisogna
cui bisogna
![\includegraphics[scale=0.25]{malthus}](img214.gif) Attraverso un esempio concreto (la dinamica della cavalletta) e un problema
proposto (la dinamica della cinciallegra) capiremo come utilizzare
l'equazione di bilancio per formulare il più semplice modello di
popolazione: quello malthusiano, così chiamato in onore di T. R. Malthus, il
fondatore della moderna demografia. Esso prevede un andamento esponenziale
dell'abbondanza di una popolazione e si basa sull'ipotesi fondamentale che
le capacità di sopravvivere e di riprodursi di ciascun individuo non
siano influenzate dalla presenza di altri individui della stessa specie.
Attraverso un esempio concreto (la dinamica della cavalletta) e un problema
proposto (la dinamica della cinciallegra) capiremo come utilizzare
l'equazione di bilancio per formulare il più semplice modello di
popolazione: quello malthusiano, così chiamato in onore di T. R. Malthus, il
fondatore della moderna demografia. Esso prevede un andamento esponenziale
dell'abbondanza di una popolazione e si basa sull'ipotesi fondamentale che
le capacità di sopravvivere e di riprodursi di ciascun individuo non
siano influenzate dalla presenza di altri individui della stessa specie.
![]() sopravvive fino all'anno
successivo, il numero di individui nella generazione
sopravvive fino all'anno
successivo, il numero di individui nella generazione ![]() sarà dato solo
dagli individui nati nella generazione
sarà dato solo
dagli individui nati nella generazione ![]() che sopravvivono fino alla
generazione
che sopravvivono fino alla
generazione ![]() . Avendo indicato con
. Avendo indicato con ![]() il numero di cavallette (maschi +
femmine) all'inizio della generazione
il numero di cavallette (maschi +
femmine) all'inizio della generazione ![]() , conviene costruire il modello per
passi successivi:
, conviene costruire il modello per
passi successivi:
![\includegraphics[width=0.7\linewidth]{serie_cavallette}](img217.gif)
![]() 0.76
0.76![]() 0.76
0.76![]() 0.89=0.37) raggiunge lo stadio di adulto
riproduttivo.
0.89=0.37) raggiunge lo stadio di adulto
riproduttivo.