Se indichiamo con Nt il numero totale di individui (maschi + femmine) all'inizio della generazione t (cioè all'inizio dell'estate, appena prima della riproduzione), la dinamica della popolazione di cinciallegre sarà descritta dalla seguente equazione:
Nt+1 = Nt - morti durante la generazione t + nuovi nati nella generazione t
Le cinciallegre che muoiono durante la generazione t sono pari 0.5Nt e quindi gli adulti della generazione t che sopravvivo fino alla generazione successiva sono semplicemente:
Nt - 0.5 Nt = 0.5 Nt
Per quanto riguarda il calcolo dei nati nella generazione t che sopravvivono fino alla generazione successiva, si procede, come nel caso precedente, per passi successivi:
|
num. femmine della generazione t: |
Nt /2 |
|
num. uova: |
10 x num. femmine = 5 Nt |
|
num. pulcini di 1 mese: |
0.84 x num. nuova = 4.2 Nt |
|
num. pulcini di 3 mesi: |
0.71 x pulcini di 1 mese = 0.71 x 4.2 Nt = 2.982 Nt |
|
num. pulcini che diventano adulti: |
0.1 x 2.982 Nt = 0.298 Nt |
La dinamica della popolazione di cinciallegre risulta allora compiutamente descritta dalla seguente equazione:
Nt+1 = 0.5 Nt + 0.298 Nt = 0.798 Nt
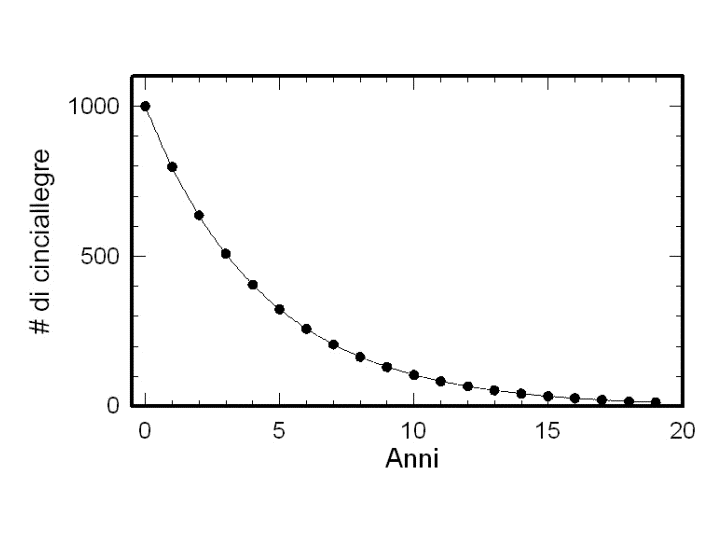
Il fattore "0.798" è il tasso finito di crescita della popolazione. Dal momento che il suo valore è inferiore a 1, la popolazione di cinciallegre diminuisce da un anno all'altro: infatti, se oggi la popolazione ha 1000 individui, l'anno prossimo ne avrà solo 798, il successivo 637 e così via (si veda la figura qui sotto).

Questa popolazione è quindi destinata ad estinguersi (perde quasi il 20% di individui ogni anno) a meno che non intervengano nuovi fattori, legati ad esempio a ripopolamenti o migrazioni, che permettano di compensare la naturale perdita di individui di Parus maior (ma in questo caso, naturalmente, si dovrebbe cambiare il modello, in quanto l'equazione che abbiamo appena ricavato non sarebbe più valida).