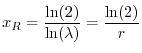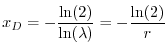Subsections
Il modello di crescita ricavato in precedenza si basa
sull'ipotesi che la riproduzione sia concentrata in una determinata stagione dell'anno.
Non per tutte le popolazioni tale approssimazione è corretta, tuttavia.
In molti casi, infatti, gli individui si riproducono con continuità nel corso dell'anno e non esiste
alcuna stagione preferenziale di accoppiamento. In queste circostanze,
occorre formulare il modello partendo dall'idea che il tempo sia una
variabile reale e non un numero intero.
Anziché scrivere l'equazione di bilancio fra una generazione e la
successiva, è dunque opportuno descrivere cosa accade in un breve
intervallo di tempo dt come
dove  indica il numero di individui al tempo
indica il numero di individui al tempo  , mentre
nascite
, mentre
nascite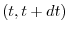 e
morti
e
morti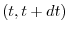 rappresentano rispettivamente il numero di individui nati e morti durante
l'intervallo di tempo di durata
rappresentano rispettivamente il numero di individui nati e morti durante
l'intervallo di tempo di durata 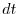 , compreso fra
, compreso fra 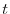 e
e 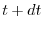 . Per calcolare il numero
complessivo di nuovi nati durante un certo intervallo di tempo bisogna
considerare che esso cresce proporzionalmente a ciascuno dei tre seguenti
fattori:
. Per calcolare il numero
complessivo di nuovi nati durante un certo intervallo di tempo bisogna
considerare che esso cresce proporzionalmente a ciascuno dei tre seguenti
fattori:
- il numero totale di individui presenti nella popolazione al tempo
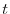 .
.
- il potenziale riproduttivo medio nell'unità di tempo (
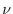 ) di ciascun
individuo comunemente chiamato tasso istantaneo di natalità.
) di ciascun
individuo comunemente chiamato tasso istantaneo di natalità.
- la durata dell'intervallo di tempo considerato (
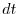 ).
).
Si può pertanto scrivere che
nascite
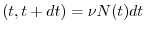
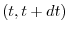 si può seguire un ragionamento
analogo al precedente. Il numero totale di morti cresce infatti
proporzionalmente a:
si può seguire un ragionamento
analogo al precedente. Il numero totale di morti cresce infatti
proporzionalmente a:
- il numero totale di individui presenti nella popolazione al tempo
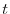 ;
;
- la probabilità media (
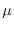 ) che un individuo ha di morire durante
l'intervallo di tempo in esame, comunemente detta tasso istantaneo di mortalità;
) che un individuo ha di morire durante
l'intervallo di tempo in esame, comunemente detta tasso istantaneo di mortalità;
- la durata dell'intervallo di tempo considerato (
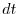 ).
).
Ne risulta dunque che:
morti
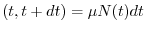
L'equazione di bilancio si può quindi riscrivere nel modo seguente:
Fattorizzando opportunamente i vari termini e riordinando i due membri
dell'equazione, si ottiene
Per intervalli di tempo infinitamente brevi, cioè valutando il limite
per 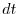 che tende a zero, si riconosce nel primo membro la derivata temporale
della grandezza
che tende a zero, si riconosce nel primo membro la derivata temporale
della grandezza 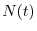 . L'equazione di bilancio, che regola la dinamica della
popolazione, diventa dunque la seguente equazione differenziale
. L'equazione di bilancio, che regola la dinamica della
popolazione, diventa dunque la seguente equazione differenziale
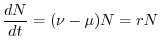 |
(6.7) |
dove, per semplicità di notazione, è stato omesso l'indice 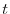 dalla
variabile
dalla
variabile 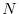 . Se
. Se 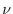 e
e 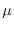 sono costanti (ipotesi malthusiana)
il parametro
sono costanti (ipotesi malthusiana)
il parametro 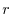 , che rappresenta la differenza fra il tasso di
natalità e quello di mortalità, viene chiamato tasso istantaneo intrinseco di crescita.
, che rappresenta la differenza fra il tasso di
natalità e quello di mortalità, viene chiamato tasso istantaneo intrinseco di crescita.
Secondo il modello malthusiano per popolazioni a dinamica continua, dunque,
la variazione nell'unità di tempo del numero di individui è
proporzionale, secondo il tasso intrinseco di crescita 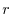 , al numero
, al numero 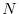 di
individui presenti nella popolazione, ovvero
di
individui presenti nella popolazione, ovvero
Tale equazione differenziale si può integrare facilmente e la sua
soluzione è la seguente
dove 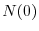 rappresenta la densità di individui nella popolazione
all'istante iniziale (
rappresenta la densità di individui nella popolazione
all'istante iniziale (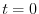 ). Ne segue che la dinamica di una popolazione a
riproduzione continua con accrescimento malthusiano è di tipo
esponenziale. Se il tasso di mortalità
). Ne segue che la dinamica di una popolazione a
riproduzione continua con accrescimento malthusiano è di tipo
esponenziale. Se il tasso di mortalità 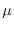 è maggiore del tasso
di natalità
è maggiore del tasso
di natalità 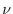 , il flusso di nascite non compensa il flusso di morti
e la popolazione è in declino, dato che
, il flusso di nascite non compensa il flusso di morti
e la popolazione è in declino, dato che 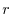 è negativo. Viceversa, se
è negativo. Viceversa, se
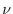 è maggiore di
è maggiore di 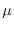 , le nascite superano le morti e la
popolazione è in crescita (
, le nascite superano le morti e la
popolazione è in crescita (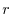 è positivo). L'andamento della soluzione
in dipendenza del segno del parametro
è positivo). L'andamento della soluzione
in dipendenza del segno del parametro 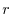 è riportato in Fig. 6.
è riportato in Fig. 6.
Figura 6:
Andamento qualitativo dell'abbondanza della
popolazione al variare di 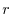
|
![\includegraphics[width=0.6\linewidth]{sugiu}](img264.gif) |
Riassumendo, dunque, se:
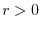 la popolazione cresce esponenzialmente
la popolazione cresce esponenzialmente
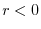 la popolazione declina esponenzialmente (estinzione certa)
la popolazione declina esponenzialmente (estinzione certa)
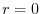 la popolazione è in uno stato stazionario (
la popolazione è in uno stato stazionario (
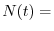 costante)
costante)
Come per la stima del tasso finito di crescita, anche per popolazioni a
riproduzione continua di cui si voglia stimare il tasso intrinseco di
crescita risulta conveniente utilizzare il metodo della regressione lineare, che si applica facilmente per via grafica. Occorre cioè
riportare su un grafico in scala semi-logaritmica l'andamento
dell'abbondanza nel tempo e valutare il tasso intrinseco come il
coefficiente angolare della retta che meglio descrive i dati. Infatti
Un esempio di stima del tasso intrinseco è riportata in Fig. 7 e riguarda la dinamica
del copepode Euterpina acutifrons. Dal momento che la retta che
meglio interpola i dati (quadratini) ha equazione
si può stimare in 0.126 giorni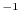 il valore del tasso intrinseco
di crescita.
il valore del tasso intrinseco
di crescita.
È facile infine riconoscere che la soluzione del modello continuo è
l'equivalente della soluzione ottenuta per popolazioni a riproduzione
concentrata. Si noti, infatti, che, se si pone
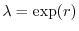 , la
soluzione del modello continuo assume la forma
, la
soluzione del modello continuo assume la forma
che è esattamente uguale alla soluzione ottenuta nel caso discreto.
Figura 7:
Andamento nel tempo del logaritmo dell'abbondanza
di Euterpina acutifrons.
|
![\includegraphics[scale=0.8]{euterpina}](img273.gif) |
Grazie all'equazione precedente possiamo calcolare facilmente quanto tempo
dobbiamo aspettare prima di osservare un raddoppiamento di una popolazione
(quando
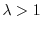 ) o un suo dimezzamento (quando
) o un suo dimezzamento (quando
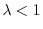 ). Se
). Se
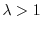 , si pone
, si pone
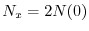 con
con 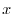 incognito, e si sostituisce questa
espressione nell'equazione (3), ottenendo così
incognito, e si sostituisce questa
espressione nell'equazione (3), ottenendo così
Dividendo membro a membro per 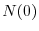 , si ha
, si ha
da cui si calcola il tempo di raddoppiamento
dove con 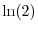 si indica il logaritmo naturale di 2. In maniera analoga, se
si indica il logaritmo naturale di 2. In maniera analoga, se
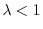 si calcola il tempo di dimezzamento come
si calcola il tempo di dimezzamento come
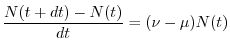
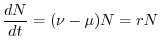
![]() , al numero
, al numero ![]() di
individui presenti nella popolazione, ovvero
di
individui presenti nella popolazione, ovvero
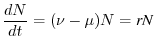
![]() , la
soluzione del modello continuo assume la forma
, la
soluzione del modello continuo assume la forma
![]() ) o un suo dimezzamento (quando
) o un suo dimezzamento (quando
![]() ). Se
). Se
![]() , si pone
, si pone
![]() con
con ![]() incognito, e si sostituisce questa
espressione nell'equazione (3), ottenendo così
incognito, e si sostituisce questa
espressione nell'equazione (3), ottenendo così