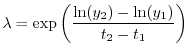Subsections
In entrambi gli esempi presentati si è pervenuti a un modello descritto
da un'equazione che può essere espressa, in termini generali, come
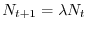 |
(6.1) |
Tale modello viene detto modello malthusiano in onore di Malthus che per primo la propose per
descrivere la crescita della popolazione umana nel suo famoso Saggio sulla Popolazione del 1798.
L'ipotesi fondamentale per ottenere una crescita malthusiana è che tutti
i parametri demografici (fertilità, sopravvivenza, ecc.) siano costanti. Come si è
visto negli esempi illustrati precedentemente, il parametro 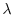 ,
detto tasso finito intrinseco di crescita, gioca un ruolo fondamentale nel determinare i
comportamenti assunti dal modello. Si può infatti affermare che
,
detto tasso finito intrinseco di crescita, gioca un ruolo fondamentale nel determinare i
comportamenti assunti dal modello. Si può infatti affermare che
- se
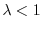 la popolazione è in declino
la popolazione è in declino
- se
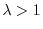 allora la popolazione è in crescita
allora la popolazione è in crescita
- se
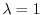 la popolazione è in stato stazionario (
la popolazione è in stato stazionario (
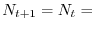 costante) .
costante) .
Noto che sia il valore del parametro 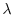 , è facile calcolare
l'abbondanza della popolazione dopo
, è facile calcolare
l'abbondanza della popolazione dopo  generazioni a partire dalla sua
abbondanza iniziale
generazioni a partire dalla sua
abbondanza iniziale 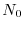 . È sufficiente, infatti, iterare per
. È sufficiente, infatti, iterare per  volte
l'uso dell'equazione (3):
volte
l'uso dell'equazione (3):
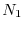 |
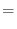 |
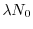 |
(6.2) |
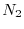 |
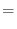 |
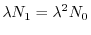 |
(6.3) |
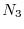 |
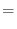 |
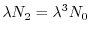 |
(6.4) |
| |
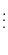 |
 |
(6.5) |
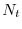 |
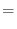 |
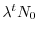 |
(6.6) |
Una popolazione a dinamica malthusiana ha pertanto un andamento
dell'abbondanza di tipo geometrico. Nel caso in cui il tasso finito di
crescita sia inferiore a uno, il modello prevede quindi l'estinzione della
popolazione. Se invece 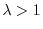 la popolazione esplode.
la popolazione esplode.
Nel caso della cavalletta e della cincia si è giunti a stimare il tasso
finito di crescita a partire dalla conoscenza dei parametri vitali della
popolazione, cioè natalità e mortalità. In altri casi è
possibile effettuare una stima di 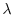 pur prescindendo dalla
conoscenza del ciclo di vita della specie, a patto di disporre di dati
relativi alle abbondanze di individui in diverse stagioni.
pur prescindendo dalla
conoscenza del ciclo di vita della specie, a patto di disporre di dati
relativi alle abbondanze di individui in diverse stagioni.
Supponiamo che siano disponibili conteggi o stime della popolazione (si veda
il paragrafo 2) in stagioni successive:
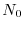 ,
, 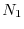 ,
, 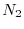 , ecc. È possibile allora stimare
, ecc. È possibile allora stimare 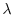 .
Essendo infatti
.
Essendo infatti
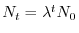 , grazie ad una trasformazione
logaritmica di entrambi i membri dell'equazione, si ottiene:
, grazie ad una trasformazione
logaritmica di entrambi i membri dell'equazione, si ottiene:
Questa non è altro che l'equazione di una retta del tipo:
dove il tempo  è la variabile indipendente (
è la variabile indipendente (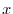 ), il logaritmo del numero
di individui nella stagione
), il logaritmo del numero
di individui nella stagione  la variabile dipendente (
la variabile dipendente (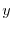 ), il logaritmo di
), il logaritmo di
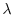 il coefficiente angolare della retta (
il coefficiente angolare della retta (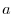 ) e il logaritmo
del numero iniziale l'intercetta della retta (
) e il logaritmo
del numero iniziale l'intercetta della retta (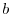 ). Nella Fig. 5 è
riportato, su un grafico in scala semi-logaritmica (avente cioè il
tempo
). Nella Fig. 5 è
riportato, su un grafico in scala semi-logaritmica (avente cioè il
tempo  in ascissa e il logaritmo di
in ascissa e il logaritmo di 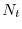 in ordinata) l'andamento
nel tempo del numero di cavallette a partire da una popolazione iniziale di
100 individui, cioè i numeri di Fig. 3. Dalla Fig. 5 si ricava che l'andamento nel tempo
del logaritmo di tali abbondanze è proprio descritto da una retta di pendenza
in ordinata) l'andamento
nel tempo del numero di cavallette a partire da una popolazione iniziale di
100 individui, cioè i numeri di Fig. 3. Dalla Fig. 5 si ricava che l'andamento nel tempo
del logaritmo di tali abbondanze è proprio descritto da una retta di pendenza
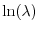 .
I dati di Fig. 3 non sono però reali, ma sono
stati generati dal modello malthusiano. Nella realtà, i dati sono affetti da errori di misura e il modello
malthusiano è solo una descrizione approssimata della dinamica
di popolazione. Non ci dobbiamo dunque aspettare che i dati allineino esattamente su una retta, ma
solo che i punti costituiscano una ``nuvola'' di forma allungata che può
ben essere approssimata da una retta.
.
I dati di Fig. 3 non sono però reali, ma sono
stati generati dal modello malthusiano. Nella realtà, i dati sono affetti da errori di misura e il modello
malthusiano è solo una descrizione approssimata della dinamica
di popolazione. Non ci dobbiamo dunque aspettare che i dati allineino esattamente su una retta, ma
solo che i punti costituiscano una ``nuvola'' di forma allungata che può
ben essere approssimata da una retta.
Figura 5:
Andamento dell'abbondanza di cavallette nel tempo in scala semi-logaritmica.
|
![\includegraphics[width=0.6\linewidth]{log_cavallette}](img241.gif) |
La pendenza di questa retta può allora essere stimata attraverso uno dei
tradizionali metodi di regressione lineare (come i minimi quadrati) ormai
disponibili in tutti i pacchetti statistici funzionanti su PC e nei fogli
elettronici commerciali più diffusi. Tale pendenza costituisce una stima
di
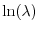 . Anche solo attraverso una semplice
calcolatrice tascabile (purché abbia le funzioni logaritmo ed
esponenziale), si può procedere manualmente in questo modo:
. Anche solo attraverso una semplice
calcolatrice tascabile (purché abbia le funzioni logaritmo ed
esponenziale), si può procedere manualmente in questo modo:
- si calcola il logaritmo di
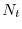 nei vari istanti di osservazione
nei vari istanti di osservazione
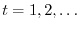 ;
;
- si riportano i dati su un grafico avente le stagioni
 in ascissa e
in ascissa e
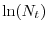 in ordinata;
in ordinata;
- si disegna ad occhio la retta interpolante (quella che cioè meglio
approssima i dati);
- si individuano le ordinate (
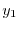 e
e 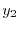 ) e le ascisse (
) e le ascisse (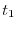 e
e
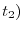 di due punti appartenenti a tale retta;
di due punti appartenenti a tale retta;
- si calcola una stima del tasso finito di crescita come:
Non possiamo aspettarci naturalmente che la stima del tasso finito di
crescita fatta ad occhio sia rigorosa, ma è un esercizio utile che si
consiglia di fare perché permette di avere comunque un'idea del valore
di 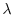 . Provate, ad esempio, a utilizzare i dati del problema
1.19 dell'eserciziario riguardanti la crescita dell'elefante di mare in
California.
. Provate, ad esempio, a utilizzare i dati del problema
1.19 dell'eserciziario riguardanti la crescita dell'elefante di mare in
California.
![]() pur prescindendo dalla
conoscenza del ciclo di vita della specie, a patto di disporre di dati
relativi alle abbondanze di individui in diverse stagioni.
pur prescindendo dalla
conoscenza del ciclo di vita della specie, a patto di disporre di dati
relativi alle abbondanze di individui in diverse stagioni.
![]() ,
, ![]() ,
, ![]() , ecc. È possibile allora stimare
, ecc. È possibile allora stimare ![]() .
Essendo infatti
.
Essendo infatti
![]() , grazie ad una trasformazione
logaritmica di entrambi i membri dell'equazione, si ottiene:
, grazie ad una trasformazione
logaritmica di entrambi i membri dell'equazione, si ottiene:
![]() . Anche solo attraverso una semplice
calcolatrice tascabile (purché abbia le funzioni logaritmo ed
esponenziale), si può procedere manualmente in questo modo:
. Anche solo attraverso una semplice
calcolatrice tascabile (purché abbia le funzioni logaritmo ed
esponenziale), si può procedere manualmente in questo modo: