Le strategie vitali delle diverse specie viventi variano considerevolmente tra i diversi
taxa. Alcune specie (si pensi ai pesci) generano molte migliaia di piccoli i quali hanno tuttavia
scarsissime probabilità sul piano individuale di raggiungere l'età adulta. Altre specie, come
i mammiferi, producono pochi cuccioli ma investono moltissime energie per garantire loro
di raggiungere la maturità. Per orientarsi in un panorama così diversificato, gli
ecologi compilano alcune tabelle (note con il nome di tabelle di vita) nelle quali
annotano il valore dei più significativi parametri demografici al crescere dell'età.
In un esperimento ideale, una tabella di vita può essere costruita come segue. Si
supponga di considerare una popolazione di nuovi nati (età 0) costituita da ![]() individui.
La grandezza
individui.
La grandezza ![]() si chiama radice della coorte, dove con il termine coorte si indica
una popolazione di individui nati contemporaneamente. Affinché l'esperimento sia significativo, è
necessario che
si chiama radice della coorte, dove con il termine coorte si indica
una popolazione di individui nati contemporaneamente. Affinché l'esperimento sia significativo, è
necessario che ![]() sia sufficientemente elevato (ad esempio pari a 1000 individui).
Per un periodo di tempo sufficientemente lungo, possibilmente con cadenza regolare,
si registrano quindi, al variare dell'età
sia sufficientemente elevato (ad esempio pari a 1000 individui).
Per un periodo di tempo sufficientemente lungo, possibilmente con cadenza regolare,
si registrano quindi, al variare dell'età ![]() , sia il numero di individui della coorte
sopravvissuti sino a quell'età (
, sia il numero di individui della coorte
sopravvissuti sino a quell'età (![]() ) che il numero di nuovi nati generati nell'unità
di tempo da ciascuno di essi (tasso di natalità
) che il numero di nuovi nati generati nell'unità
di tempo da ciascuno di essi (tasso di natalità ![]() ). In demografia è spesso conveniente descrivere
la dinamica della sola popolazione femminile, poiché il rapporto sessi
è praticamente costante. La fertilità viene quindi solitamente
espressa come numero di nuovi piccoli di sesso femminile prodotti da ogni madre.
Un tipico esempio di tabella di vita è riportato in Tab. 1.
). In demografia è spesso conveniente descrivere
la dinamica della sola popolazione femminile, poiché il rapporto sessi
è praticamente costante. La fertilità viene quindi solitamente
espressa come numero di nuovi piccoli di sesso femminile prodotti da ogni madre.
Un tipico esempio di tabella di vita è riportato in Tab. 1.
| (anni) | (# indiv.) | (anni |
(anni) | (# indiv.) | (anni |
|
| 0 | 1000 | 0 | 8 | 104 | 0.642 | |
| 1 | 490 | 0 | 9 | 69 | 2.413 | |
| 2 | 396 | 0 | 10 | 41 | 2.345 | |
| 3 | 324 | 0 | 11 | 14 | 2.886 | |
| 4 | 283 | 0 | 12 | 11 | 5.914 | |
| 5 | 264 | 0.016 | 13 | 8 | 4.513 | |
| 6 | 202 | 0.038 | 14 | 2 | 0 | |
| 7 | 139 | 0.134 |
Dalle tabelle di vita possono venire ricavate diverse informazioni
di grande interesse. Le principali funzioni demografiche che si estraggono dalle tabelle di vita sono
la probabilità di sopravvivenza ![]() , la vita media
, la vita media ![]() , la funzione netta di maternità
, la funzione netta di maternità
![]() e il tasso netto di riproduzione
e il tasso netto di riproduzione ![]() .
.
In ecologia delle popolazioni si indica solitamente con ![]() la probabilità
che ciascun individuo ha alla nascita di sopravvivere almeno sino all'età
la probabilità
che ciascun individuo ha alla nascita di sopravvivere almeno sino all'età ![]() .
Se si indica con
.
Se si indica con ![]() il tasso di mortalità all'età
il tasso di mortalità all'età ![]() , ovvero la probabilità di morte
di un individuo di età
, ovvero la probabilità di morte
di un individuo di età ![]() nell'infinitesimo intervallo di età
nell'infinitesimo intervallo di età ![]() ,
si può impostare facilmente l'equazione che consente di determinare
,
si può impostare facilmente l'equazione che consente di determinare ![]() come
come
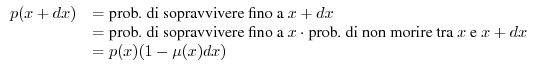
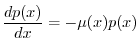
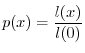
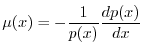
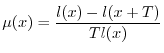
Data la forma della (6), si osserva che la funzione di sopravvivenza ![]() deve necessariamente decrescere con l'età, perché la mortalità
deve necessariamente decrescere con l'età, perché la mortalità ![]() non può
essere negativa. L'andamento di
non può
essere negativa. L'andamento di ![]() può tuttavia essere qualitativamente molto diverso a
seconda delle popolazioni in esame. Per meglio apprezzare i possibili andamenti della mortalità con
l'età in popolazioni reali, in Fig. 3 viene riportato l'andamento del logaritmo
naturale di
può tuttavia essere qualitativamente molto diverso a
seconda delle popolazioni in esame. Per meglio apprezzare i possibili andamenti della mortalità con
l'età in popolazioni reali, in Fig. 3 viene riportato l'andamento del logaritmo
naturale di ![]() in funzione dell'età
in funzione dell'età ![]() per tre popolazioni differenti.
Ricordando la forma esponenziale della (6),
si comprende che, se la mortalità fosse costante con l'età, l'andamento
del
per tre popolazioni differenti.
Ricordando la forma esponenziale della (6),
si comprende che, se la mortalità fosse costante con l'età, l'andamento
del
![]() dovrebbe essere approssimativamente
lineare. Questo è il caso di molte specie di uccelli, come la
pavoncella di Fig. 3b: il rischio di morte
di un uccello, se legato all'attività di volo, non dipende
infatti dal fattore età. Nei casi di alta sopravvivenza fra le larve o fra i giovani, come
nel caso della mosca della frutta di Fig. 3a,
il decremento di
dovrebbe essere approssimativamente
lineare. Questo è il caso di molte specie di uccelli, come la
pavoncella di Fig. 3b: il rischio di morte
di un uccello, se legato all'attività di volo, non dipende
infatti dal fattore età. Nei casi di alta sopravvivenza fra le larve o fra i giovani, come
nel caso della mosca della frutta di Fig. 3a,
il decremento di ![]() è meno che esponenziale. Molto comune
tuttavia tra gli insetti, i crostacei, i celenterati, i pesci e le piante
- cioè fra quegli organismi che producono molte uova o semi e/o che hanno
uno stadio larvale seguito da una metamorfosi ad uno stadio adulto - è un decremento
della mortalità con l'età, come nel caso del ranuncolo dei prati di
Fig. 3c. Dei molti propaguli prodotti, infatti, moltissimi
muoiono nelle prime fasi del ciclo di vita. Classicamente (Deevey, 1947)
le tre tipologie di funzione di sopravvivenza appena descritte sono denominate
di tipo I (
è meno che esponenziale. Molto comune
tuttavia tra gli insetti, i crostacei, i celenterati, i pesci e le piante
- cioè fra quegli organismi che producono molte uova o semi e/o che hanno
uno stadio larvale seguito da una metamorfosi ad uno stadio adulto - è un decremento
della mortalità con l'età, come nel caso del ranuncolo dei prati di
Fig. 3c. Dei molti propaguli prodotti, infatti, moltissimi
muoiono nelle prime fasi del ciclo di vita. Classicamente (Deevey, 1947)
le tre tipologie di funzione di sopravvivenza appena descritte sono denominate
di tipo I (![]() crescente con
crescente con ![]() come in Fig. 3a),
tipo II (
come in Fig. 3a),
tipo II (
![]() costante come in Fig. 3b)
e tipo III (
costante come in Fig. 3b)
e tipo III (![]() decrescente come in Fig. 3c).
decrescente come in Fig. 3c).
![\includegraphics[scale=1]{sopravvivenze}](img302.gif) |
I tre tipi descritti non esauriscono tutti i casi di curve di sopravvivenza, in quanto esistono popolazioni di moltissime specie, per esempio di mammiferi, in cui la mortalità prima decresce (mortalità neonatale) e poi cresce con l'età (vecchiaia). Secondo Slobodkin (1961) la curva di tipo III è la più comune in natura mentre l'uomo adulto nei paesi sviluppati come il nostro avrebbe una curva di sopravvivenza di tipo I, ipotesi fatta propria da Krebs (1972) e confermata da molti dati.
Una grandezza molto importante che si puó ricavare dalla funzione di sopravvivenza
é la lunghezza media della vita che un individuo deve attendersi di vivere
quando nasce, detta vita media alla nascita e indicata con ![]() .
Per calcolarla si può fare il seguente ragionamento. Le unità di tempo vissute dalla totalità degli individui durante
l'intervallo di età
.
Per calcolarla si può fare il seguente ragionamento. Le unità di tempo vissute dalla totalità degli individui durante
l'intervallo di età
![]() sono
sono
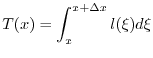
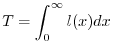
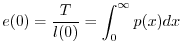 |
(7.2) |
Da una tabella di vita viene anche ricavato il tasso di natalità ![]() che è definito come segue
che è definito come segue
Conoscere ![]() consente di ricavare il cosiddetto tasso netto di riproduzione
consente di ricavare il cosiddetto tasso netto di riproduzione ![]() .
Tale parametro demografico è definito come il numero medio di figlie prodotto da una femmina nel corso della sua
vita. Esso si ottiene perciò molto semplicemente integrando la funzione netta
di maternità, cioè
.
Tale parametro demografico è definito come il numero medio di figlie prodotto da una femmina nel corso della sua
vita. Esso si ottiene perciò molto semplicemente integrando la funzione netta
di maternità, cioè