Se la terra fosse priva di atmosfera sarebbe praticamente una palla di
ghiaccio. Non è difficile ricavare con un semplice ragionamento
termodinamico che la sua temperatura superficiale media sarebbe ben al di
sotto di 0![]() C. Infatti la temperatura risulterebbe dall'equilibrio tra
la radiazione solare incidente e l'irraggiamento della terra come mostrato
in Fig. 1. Il flusso di calore entrante è dovuto all'assorbimento
della radiazione solare incidente che è sostanzialmente dominata da
lunghezze d'onda corte (luce visibile) mentre il flusso di calore uscente
è dovuto all'irraggiamento della terra ed è sostanzialmente dominato
da lunghezze d'onda più lunghe (radiazione infrarossa).
C. Infatti la temperatura risulterebbe dall'equilibrio tra
la radiazione solare incidente e l'irraggiamento della terra come mostrato
in Fig. 1. Il flusso di calore entrante è dovuto all'assorbimento
della radiazione solare incidente che è sostanzialmente dominata da
lunghezze d'onda corte (luce visibile) mentre il flusso di calore uscente
è dovuto all'irraggiamento della terra ed è sostanzialmente dominato
da lunghezze d'onda più lunghe (radiazione infrarossa).
Grazie alla prima legge della termodinamica, possiamo scrivere
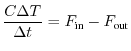
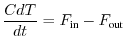
Il flusso
![]() può invece essere determinato a partire dalla legge
di Stefan-Boltzmann. Secondo tale legge la radiazione di un corpo avente una
certa temperatura (la cosiddetta radiazione di corpo nero) aumenta con la quarta potenza della
temperatura assoluta del corpo radiante. In particolare la potenza emessa
per unità di superficie da un perfetto corpo nero a temperatura
può invece essere determinato a partire dalla legge
di Stefan-Boltzmann. Secondo tale legge la radiazione di un corpo avente una
certa temperatura (la cosiddetta radiazione di corpo nero) aumenta con la quarta potenza della
temperatura assoluta del corpo radiante. In particolare la potenza emessa
per unità di superficie da un perfetto corpo nero a temperatura ![]() è
pari a
è
pari a
![]() con
con
![]() W m
W m
![]() . La
terra è in realtà un corpo ``grigio'', ma in prima approssimazione
possiamo usare l'espressione teorica di Stefan-Boltzmann e quindi ottenere
il flusso uscente semplicemente moltiplicando per la superficie terrestre
(
. La
terra è in realtà un corpo ``grigio'', ma in prima approssimazione
possiamo usare l'espressione teorica di Stefan-Boltzmann e quindi ottenere
il flusso uscente semplicemente moltiplicando per la superficie terrestre
(
![]() )
)
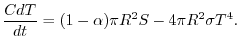
In condizioni di equilibrio, cioè per ![]() , il flusso di calore entrante
deve uguagliare quello uscente e pertanto si ha
, il flusso di calore entrante
deve uguagliare quello uscente e pertanto si ha
Per fortuna la terra, a differenza della luna, ha una massa tale da
garantire un'attrazione gravitazionale sufficiente a contrastare in modo
efficace i movimenti casuali delle molecole di gas. In questa maniera le
molecole gassose sono trattenute vicino alla crosta terrestre e formano
l'atmosfera. L'atmosfera con tutti i suoi gas componenti (vedi Tab. 1.1)
e le nuvole alterano il semplice quadro termodinamico tratteggiato prima.
Attraverso un effetto simile a quello di una serra, la terra è in grado di
catturare calore nell'atmosfera e di mantenere così la temperatura
superficiale media a circa 15![]() C.
C.
| Costituente | Formula | Peso molecolare | Volume (%) | Massa totale |
| chimica | ( |
in aria secca | (grammi) | |
| Atmosfera totale | -- | -- | -- | 5.136 |
| Vapore acqueo | H |
18.01 | variabile | 0.017 |
| Aria secca | -- | 28.96 | 100 | 5.119 |
| Azoto | N |
28.01 | 78.08 | 3.866 |
| Ossigeno | O |
32 | 20.948 | 1.185 |
| Argo | Ar | 39.95 | 0.934 | 6.59 |
| Anidride carbonica | CO |
44 | 0.0315 | 2.45 |
| Neon | Ne | 20.18 | 1.18 |
6.48 |
| Elio | He | 4 | 5.4 |
3.71 |
| Metano | CH |
16.04 |
|
|
| Idrogeno | H |
3.01 |
|
|
| Protossido d'azoto | N |
44.01 |
|
|
| Monossido di carbonio | CO | 28.01 |
|
|
| Ammoniaca | NH |
17.03 |
|
|
| Biossido di azoto | NO |
46 |
|
|
| Anidride solforosa | SO |
64.06 |
|
|
| Acido solfidrico | H |
34.08 |
|
|
| Ozono | O |
47.99 | variabile |
|
Il bilancio delle radiazioni incidenti, assorbite e irraggiate dalla terra è presentato in Fig. 2. Viene fatta pari a 100 unità la radiazione solare incidente, la quale è sostanzialmente dominata da lunghezze d'onda corte. Di queste 100 unità, 23 sono assorbite dall'atmosfera, 31 sono riflesse come onde corte dall'aria, dalle nubi e dalla superficie terrestre e 46 sono assorbite dalla superficie terrestre. Poiché la temperatura terrestre è approssimativamente in equilibrio, bisogna che il flusso uscente dalla superficie terrestre sia anch'esso pari a 46 unità. Di queste, 7 unità vanno a riscaldare direttamente l'atmosfera (calore sensibile), 24 vanno nell'evaporazione delle masse d'acqua (il cosiddetto calore latente) e infine 15 sono irraggiate dalla terra sotto forma di onde lunghe (radiazione infrarossa). Una parte di queste onde lunghe (6 unità) è catturata dalle nubi, dal vapor d'acqua, dall'ozono, dall'anidride carbonica, dal protossido d'azoto (ossido nitroso) e dal metano. Ecco perché si dice che questi sono dei gas serra: essi sono infatti in grado di trattenere il calore nell'atmosfera. È da notare che anche l'atmosfera (nubi, vapor d'acqua e vari gas componenti) è pure all'incirca in equilibrio termico: poiché essa riceve 23 unità direttamente dal sole e 37 dalla terra (6 come onde lunghe, 7 come calore sensibile e 24 come calore latente), ci deve essere necessariamente un'emissione di 60 unità dell'atmosfera verso lo spazio esterno. Infatti 20 unità sono emesse sotto forma di onde lunghe dalle nubi e 40 dal vapor d'acqua, dall'ozono e dall'anidride carbonica.
Paragonare l'atmosfera ad una serra non è del tutto appropriato: in una serra, infatti, l'aria è sostanzialmente ferma, mentre come ben sappiamo l'atmosfera terrestre è caratterizzata da forti movimenti convettivi che sono dovuti sia alla rotazione della terra sia al fatto che l'aria più calda è più leggera di quella fredda e tende quindi a muoversi verso l'alto. In primissima approssimazione, possiamo però trascurare questi movimenti e cercare di capire come variano la pressione e la temperatura con la quota in una colonna d'aria sostanzialmente immobile.
![\includegraphics[width=0.8\linewidth]{serra}](img111.gif) |
Vediamo come si può dedurre l'andamento della pressione. Consideriamo
una colonna d'aria in cui ogni volumetto d'aria (vedi Fig. 3) è in
equilibrio meccanico. Indichiamo con ![]() l'altezza relativa al livello del mare
a cui si trova un volumetto infinitesimo di area
l'altezza relativa al livello del mare
a cui si trova un volumetto infinitesimo di area ![]() e di spessore
e di spessore ![]() e cerchiamo
di determinare come varia la pressione
e cerchiamo
di determinare come varia la pressione ![]() in funzione di
in funzione di ![]() . Sul volumetto di
densità
. Sul volumetto di
densità ![]() (ricordiamo che
(ricordiamo che ![]() è una massa per unità di volume) si
esercita in direzione verticale una forza peso pari a
è una massa per unità di volume) si
esercita in direzione verticale una forza peso pari a
![]() (con
(con ![]() indichiamo
l'accelerazione di gravità) e due forze dovute alle pressioni sulla
faccia inferiore e sulla faccia superiore del volumetto: i moduli di tali
forze valgono rispettivamente
indichiamo
l'accelerazione di gravità) e due forze dovute alle pressioni sulla
faccia inferiore e sulla faccia superiore del volumetto: i moduli di tali
forze valgono rispettivamente ![]() e
e ![]() . Perché il volumetto sia in
equilibrio meccanico dobbiamo avere
. Perché il volumetto sia in
equilibrio meccanico dobbiamo avere
Passando al limite per ![]() , otteniamo che la pressione deve soddisfare
la seguente semplice equazione differenziale
, otteniamo che la pressione deve soddisfare
la seguente semplice equazione differenziale
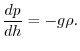
Questa equazione non è tuttavia sufficiente a determinare come varia la pressione, perché dovremmo sapere come varia la densità dell'aria con l'altezza e la densità dipende dalla pressione medesima, dalla temperatura, ecc. Possiamo però supporre che l'aria sia praticamente assimilabile a un gas perfetto e che quindi valga per essa la legge dei gas perfetti che lega pressione, volume e temperatura secondo la relazione (valevole per una mole di gas)
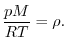
Possiamo perciò derivare come varia il gradiente di pressione in funzione della pressione medesima e della temperatura:
Sotto l'ipotesi estremamente semplificativa che la temperatura della colonna
d'aria sia costante con la quota, l'equazione (1) è lineare in ![]() e quindi
la sua soluzione è una semplice funzione esponenziale. Perciò si
ottiene che la pressione dell'aria diminuisce esponenzialmente con la quota
ovvero
e quindi
la sua soluzione è una semplice funzione esponenziale. Perciò si
ottiene che la pressione dell'aria diminuisce esponenzialmente con la quota
ovvero

Nella realtà, la temperatura non è per nulla costante con la quota: sappiamo benissimo che andando in montagna l'aria si raffredda. Nonostante la forte approssimazione introdotta, il modello di colonna isoterma funziona comunque piuttosto bene per descrivere la variazione di pressione con la quota. Si osserva infatti sperimentalmente proprio un declino esponenziale della pressione con la quota: si ha che più o meno vale la relazione
Più complicato è cercare di determinare anche approssimativamente il profilo di temperatura. A questo scopo bisognerebbe anche considerare la termodinamica di ogni volumetto di atmosfera e non solo la meccanica. Una buona approssimazione è quella in cui la colonna viene considerata adiabatica, ovvero senza scambi di calore con l'esterno; nel caso si utilizzi una colonna adiabatica umida (in cui si tiene anche conto del calore latente) il gradiente di temperatura è di circa 0.6 gradi ogni 100 metri. Ci limitiamo qui a descrivere qual è il profilo di temperatura sperimentalmente osservato (vedi Fig. 4), spiegando a grandi linee le ragioni di tale andamento. Essenzialmente si può dividere l'atmosfera nei seguenti quattro strati che sono proprio individuati dai diversi gradienti di temperatura che li caratterizzano.
![\includegraphics[scale=0.15]{temperatura}](img134.gif) |