Misurare la biodiversità

La più semplice maniera di misurare la diversità di una comunità ecologica è forse quella di contare il numero di specie che ne fanno parte. Abbiamo già detto che questo è molto riduttivo, tuttavia va notato che anche la semplice attribuzione di questo solo numero a un ecosistema implica comunque uno sforzo notevolissimo, ovvero la raccolta di un campione di organismi sufficientemente rappresentativo di tutte le specie della comunità e il riconoscimento delle specie a cui appartengono i diversi organismi. Il campione stesso, però, fornisce delle ulteriori informazioni e precisamente le abbondanze relative delle diverse specie, cioè le percentuali con cui le varie specie sono presenti nel campione e quindi, se il campione è statisticamente significativo, nella comunità. È facile capire che anche le abbondanze relative, oltre al numero di specie, concorrono a definire il grado di diversità di un ecosistema. Consideriamo infatti due comunità ciascuna contenente dieci specie, ma in cui la prima sia caratterizzata da specie aventi tutte la stessa abbondanza (10% del totale), mentre la seconda è dominata da una specie cui appartiene il 95% degli organismi del campione con le restanti nove specie concentrate nel rimanente 5%. Tutti attribuirebbero intuitivamente un maggior grado di diversità alla prima comunità. Per risolvere questo problema e descrivere la diversità ecologica in maniera più efficace che non con il solo numero di specie vengono, perciò, utilizzati indici di diversità che tengono conto anche delle abbondanze relative.

Il problema di definire la diversità non è tipico solo dell'ecologia, ma di innumerevoli altre discipline e insorge tutte le volte che si abbia un insieme di elementi ciascuno dei quali è attribuibile a una categoria (nel nostro caso la specie, ma potremmo considerare anche altre categorizzazioni come il colore, l'età, la dimensione, tutti valori che contribuiscono alla diversità ecologica). È spontaneo allora cercare di stabilire se questo insieme sia uniforme o diversificato rispetto ad una certa proprietà tipica dei suoi elementi. Quando ciascuna categoria sia associabile a una variabile casuale (ad esempio l'altezza degli alberi) la varianza del campione fornisce una semplice misura di diversità, in quanto misura il grado di scostamento dal valore medio. Ma quando le categorie sono di tipo qualitativo, come le specie di una comunità, non è possibile associare ad esse una variabile casuale in maniera naturale e i concetti di media e di varianza perdono senso. Tuttavia il concetto di diversità, come spiegato precedentemente, rimane intuitivamente ancora valido. Come possiamo definire un indice di diversità a partire dalle percentuali con cui ciascuna categoria è rappresentata nel campione? Questo problema è stato risolto per la prima volta nell'ambito della teoria dell'informazione indipendentemente da Shannon e da Wiener, che hanno definito il contenuto informativo di un messaggio costituito da diversi simboli sulla base della diversità del messaggio medesimo (ad es. un foglio contenente solo "a" ha sicuramente ben poco da dirci rispetto a un foglio che contenga una miscela di "a", "b", "c" e così via). Margalef (1958) è stato il primo ad applicare questi concetti alle discipline ecologiche. Prima di illustrare alcuni semplici concetti di base, va precisato che quanto esporremo si applica al caso in cui il campione di organismi raccolto sia molto grande, sia cioè rappresentativo di tutte le specie contenute effettivamente nell'ecosistema studiato. Quando il campione sia finito i ragionamenti vanno opportunamente modificati (per maggiori dettagli si veda il libro di Pielou, 1977).

Immaginiamo di avere raccolto un campione di organismi appartenenti ad una certa comunità. Naturalmente supponiamo che la raccolta sia stata fatta in maniera corretta senza privilegiare particolari zone dell'ecosistema o particolari specie. Abbiamo perciò un insieme di $N$ organismi che sono stati classificati in $S$ categorie (ad es. specie). Indichiamo con $p_{i}$ la probabilità che un individuo della comunità preso a caso appartenga alla specie $i$ ( $i = 1, 2, \ldots, S$). Poiché abbiamo assunto che il campione di organismi raccolti è rappresentativo dell'intera comunità possiamo dire che

$$p_{i}=\frac{N_{i}}{N}$$

dove $N_{i}$ è il numero di organismi nel campione che appartengono alla specie $i$. Un indice di diversità è una funzione $H$ delle abbondanze relative $p_{i}$ che soddisfi almeno a queste due condizioni:

1. Per un dato numero di specie $S$ la funzione $H$ assume il suo più grande valore quando le abbondanze relative sono tutte uguali, ovvero quando le specie sono equidistribuite. Se indichiamo il valore massimo con $L(S)$, deve perciò risultare
   $$L(S)=H\left(\frac{1}{S}, \frac{1}{S}, \ldots, \frac{1}{S}\right)$$

2. La diversità della comunità deve rimanere invariata se assumiamo l'esistenza di altre specie $S+1$, $S+2$, ecc. che siano fittizie, cioè a cui non appartenga nessun organismo della comunità ($p_{i} = 0$, per $i = S+1, S+2,$ ecc.). Dobbiamo perciò avere
   $$H(p_{1}, p_{2}, \ldots, p_{S}, 0, \ldots, 0) = H(p_{1}, p_{2}, \ldots, p_{S}).$$

È interessante notare che la condizione 2 insieme alla condizione 1 garantisce che di due comunità con diverso numero di specie, ma comunque equidistribuite (ogni specie ha la stessa abbondanza relativa), la comunità col maggior numero di specie ha indice di diversità più grande. Risulta infatti:

$$L(S)=H\left(\frac{1}{S}, \frac{1}{S}, \ldots, \frac{1}{S}\right)= H\left(\frac{1}{S}, \frac{1}{S}, \ldots, \frac{1}{S}, 0\right)$$

ma

$$H\left(\frac{1}{S}, \frac{1}{S}, \ldots, \frac{1}{S}, 0\right) <... ...rac{1}{S+1}, \frac{1}{S+1}, \ldots, \frac{1}{S+1}, \frac{1}{S+1}\right)=L(S+1)$$

È così rispettato uno dei requisiti che intuitivamente vanno attribuiti a un indice di diversità ecologica: una comunità con maggior numero di specie è più diversa di un'altra con minor numero a parità di distribuzione delle abbondanze.

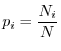
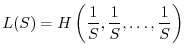
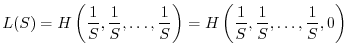
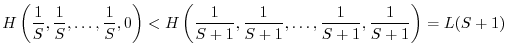
Le condizioni 1 e 2 non definiscono univocamente un buon indice di diversità. Esistono infatti infinite funzioni che soddisfano ai due requisiti. Tra di esse tuttavia le più utilizzate sono le due seguenti:

i)

l'indice di diversità di Shannon-Wiener;

ii)

l'indice di diversità di Simpson.

L'indice di Shannon è stato sviluppato nell'ambito della teoria dell'informazione e soddisfa ad altre condizioni su cui non vale la pena di soffermarsi. Esso è dato da

$$H_{SH}=-\sum_{i=1}^{S}p_i\log_2{p_i}$$

L'utilizzo del logaritmo in base 2 è semplicemente dovuto a ragioni storiche (l'uso dei bit nell'ambito della teoria dell'informazione). Usando altre basi si moltiplica semplicemente l'indice per una costante ( $\log_{2}(x) = \ln(x)/\ln(2) = \log_{10}(x)/\log_{10}(2)$).

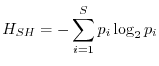
È possibile mostrare che il massimo dell'indice di Shannon (naturalmente col vincolo che $\sum_{i=1}^S p_i=1$) è raggiunto proprio in corrispondenza di $p_{i} = 1/S$ per ogni $i$, cioè che la condizione 1 è verificata. Risulta perciò

$$L(S)=-S\left(\frac{1}{S}\log_2\frac{1}{S}\right)=\log_2S$$

che ovviamente è una funzione crescente del numero di specie $S$. Anche la condizione 2 è verificata perché l'indice è una sommatoria di addendi ciascuno dei quali si annulla per $p_{i} = 0$.

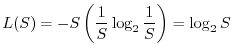
L'indice di Simpson, pur essendo meno noto di quello di Shannon, ha il vantaggio di una semplice interpretazione intuitiva. Simpson (1949), per definire la diversità, si pose la semplice domanda: qual è la probabilità che due organismi presi a caso in una determinata comunità siano della stessa specie? Se una persona va a spasso per un bosco italiano, la probabilità che due alberi presi a caso siano della stessa specie è molto più alta che se questa medesima persona si reca nella foresta amazzonica. È possibile perciò definire un indice di diversità come la probabilità che due organismi presi a caso in una certa comunità non siano della stessa specie. In formule

$$H_{SI}=1-\sum_{i=1}^{S}p_i^2$$

poichè $p_i^2$ è la probabilità di scegliere a caso due organismi della stessa specie $i$, mentre $\sum_{i=1}^S p_i^2$ è la probabilità di scegliere a caso due organismi della stessa specie, una qualsiasi tra le $S$ disponibili. Anche per l'indice di Simpson si può dimostrare che il massimo (col vincolo che $\sum_{i=1}^S p_i=1$) è raggiunto proprio in corrispondenza di $p_{i} = 1/S$ per ogni $i$. Perciò

$$L(S)=1-S\left(\frac{1}{S}\right)^2=1-\frac{1}{S}$$

che è una funzione crescente di $S$. La condizione 2 è ovviamente soddisfatta.

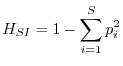
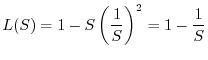
A differenza dell'indice di Shannon, che può variare tra 0 e $\infty$, l'indice di Simpson è compreso tra 0 e 1, poiché $L(S)$ è minore dell'unità. L'indice di Shannon, a causa della presenza del logaritmo, dà relativamente più peso, rispetto all'indice di Simpson, alle specie rare.

Gli indici di diversità, come abbiamo messo in evidenza, riflettono sia il numero di specie della comunità sia la maniera con cui gli organismi sono distribuiti tra le varie specie. A volte può essere utile tenere distinti i due aspetti. A questo fine si possono introdurre gli indici di equiripartizione $E$, definiti nella seguente maniera:

$$E=\frac{H\left(p_1, p_2, \ldots, p_S\right)}{L(S)}$$

Gli indici di equiripartizione, su una scala da 0 a 1, dicono quanto una comunità, a prescindere dal numero di specie che contiene, si avvicina al caso ideale della perfetta equiripartizione ($H=L(S)$). Nel caso dell'indice di Shannon si ha

$$E_{SH}=\frac{-\sum_{i=1}^{S}p_i\log_2{p_i}}{\log_2S}$$

nel caso dell'indice di Simpson si ha

$$E_{SI}=\frac{1-\sum_{i=1}^{S}p_i^2}{1-\frac{1}{S}}$$

La Tab. 1 presenta un esempio di calcolo di indici di diversità e di equiripartizione con riferimento alla comunità di rotiferi (un'importante componente dello zooplankton) del fiume Po campionata da Ferrari e Mazzoni (1989).

Tabella 1: Esempio di calcolo degli indici di diversità di Shannon e di Simpson e dei relativi indici di equiripartizione per una comunità di rotiferi campionati nel fiume Po il 23-7-1985 in località Viadana (MN) (da Ferrari e Mazzoni, 1989)

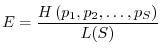
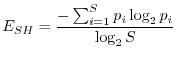
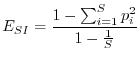
Brachionus angularis	25		L. (M.) closterocerca	25
B. bennini	525		L. (M.) hamata	1
B. calyciflorus	700		Cephalodella sp.	25
B. quadridentatus	75		Trichocerca pusilla	50
B. urceolaris	25		Synchaeta sp.	125
Brachionus m.	25		Polyarthra dolich-vulgaris	325
Keratella cochlearis	50		Asplanchna brightwelli	25
Keratella cochlearis tecta	50		A. priodonta	25
Keratella tropica	25		Filinia longiseta	25
Anuraeopsis fissa	150		Flosculariidae	1
Lepadella sp.	25		Bdelloidei	1
L. (Monostyla) sp.	50		Rotiferi non identificati	75
L. (M.) bulla	1
Numero totale di specie $S$		25
Numero totale di individui $N$		2429
Indice di Shannon $H_{\text{SH}}$		3.321
Indice di Simpson $H_{\text{SI}}$		0.841
Indice di equiripartizione (Shannon) $E_{\text{SH}}$		3.321/$\log_2(S)$=0.715
Indice di equiripartizione (Simpson) $E_{\text{SI}}$		0.841/(1-1/$S$)=0.876